Finding the Kth biggest using Heap Sort
- Sort it by getting the biggest, then the next biggest, then the next and so on. . .
- Every time to get the next biggest – get the biggest and fix the heap takes —-> logn
Hence, for kth biggest –> klogn
2nd biggest—>2logn
3rd biggest —>3logn
Middle one —> (n/2)logn
(we want this in linear time)
Note: Calculating the median is a special case of finding the kth biggest element.
Method to calculate the median (or) to find the kth biggest element
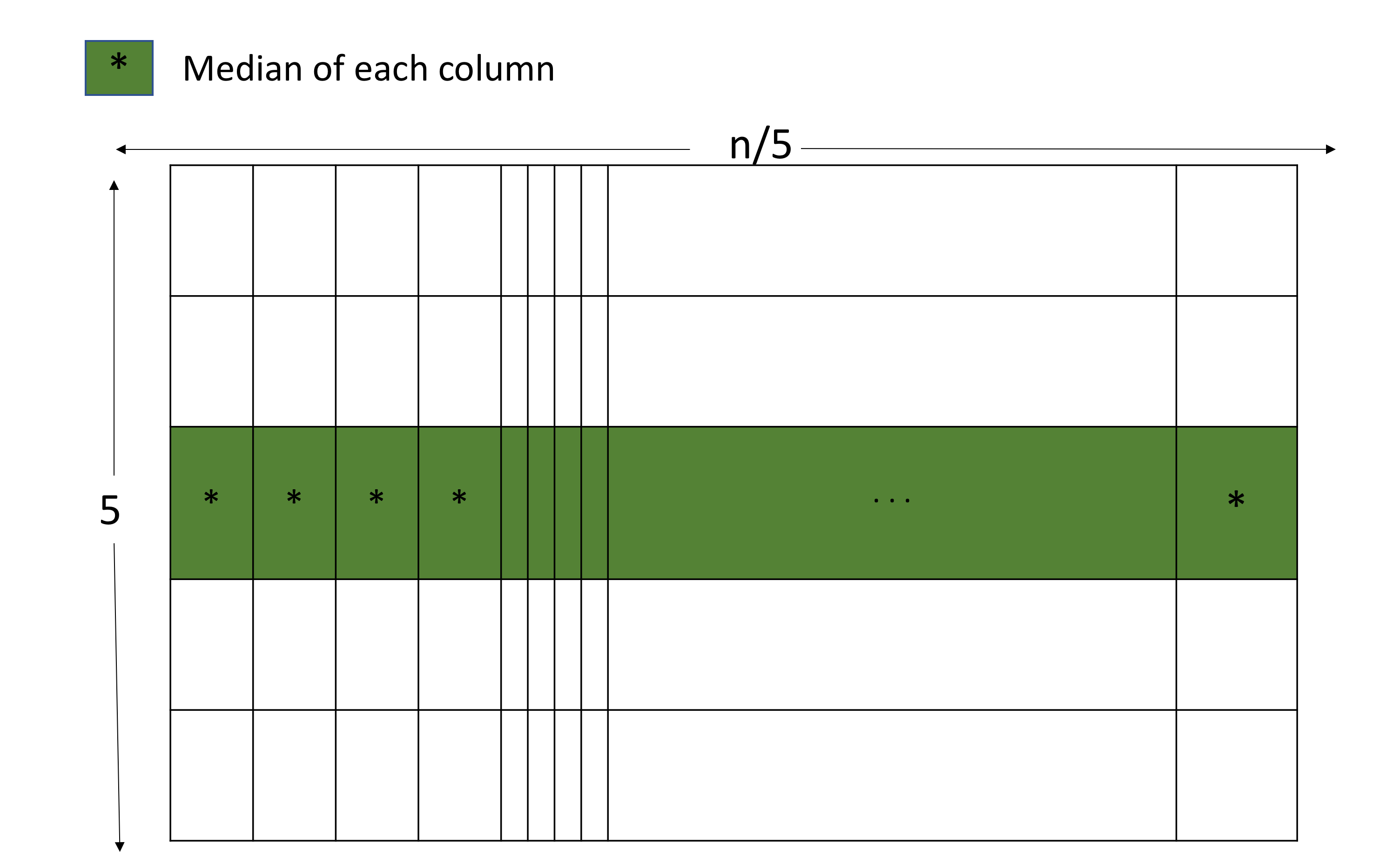
Fill the numbers in a 2D array with 5 rows and ‘n/5’ columns, where ‘n’ is the number of elements in your list.
Goal is to find the middle element in each column.
Steps:
- Find the middle element in each column.(it takes 6 comparisons for 5 elements).
- Partition the column such that smaller ones are above and larger ones are below the middle element.(constant number of moves since there are only 5 elements)
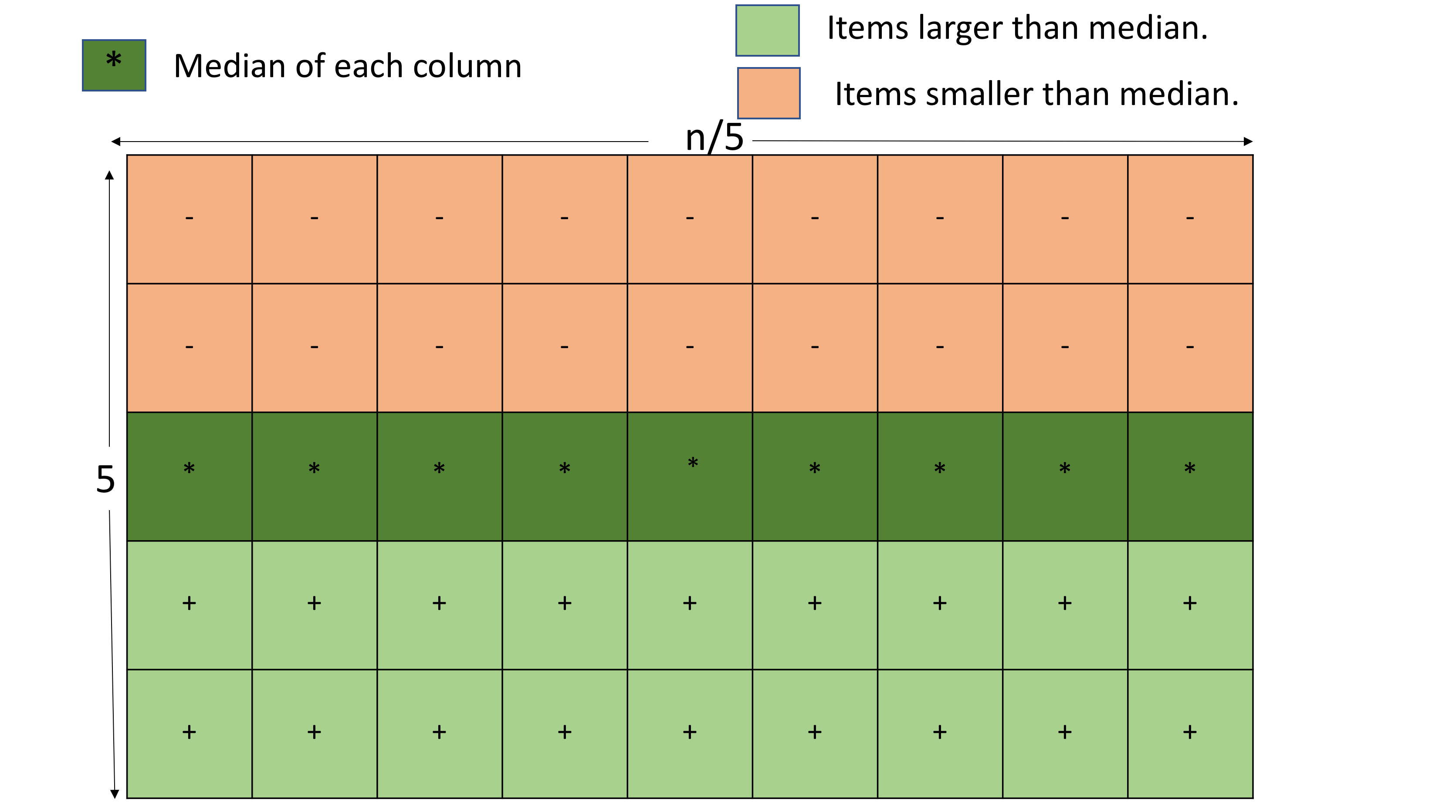
- Find the median of middle row and partition it left to right(as in Quick Sort) such that smaller elements are on left and bigger ones are on the right of the median.
Move the complete length 5 columns around appropriately after the partition.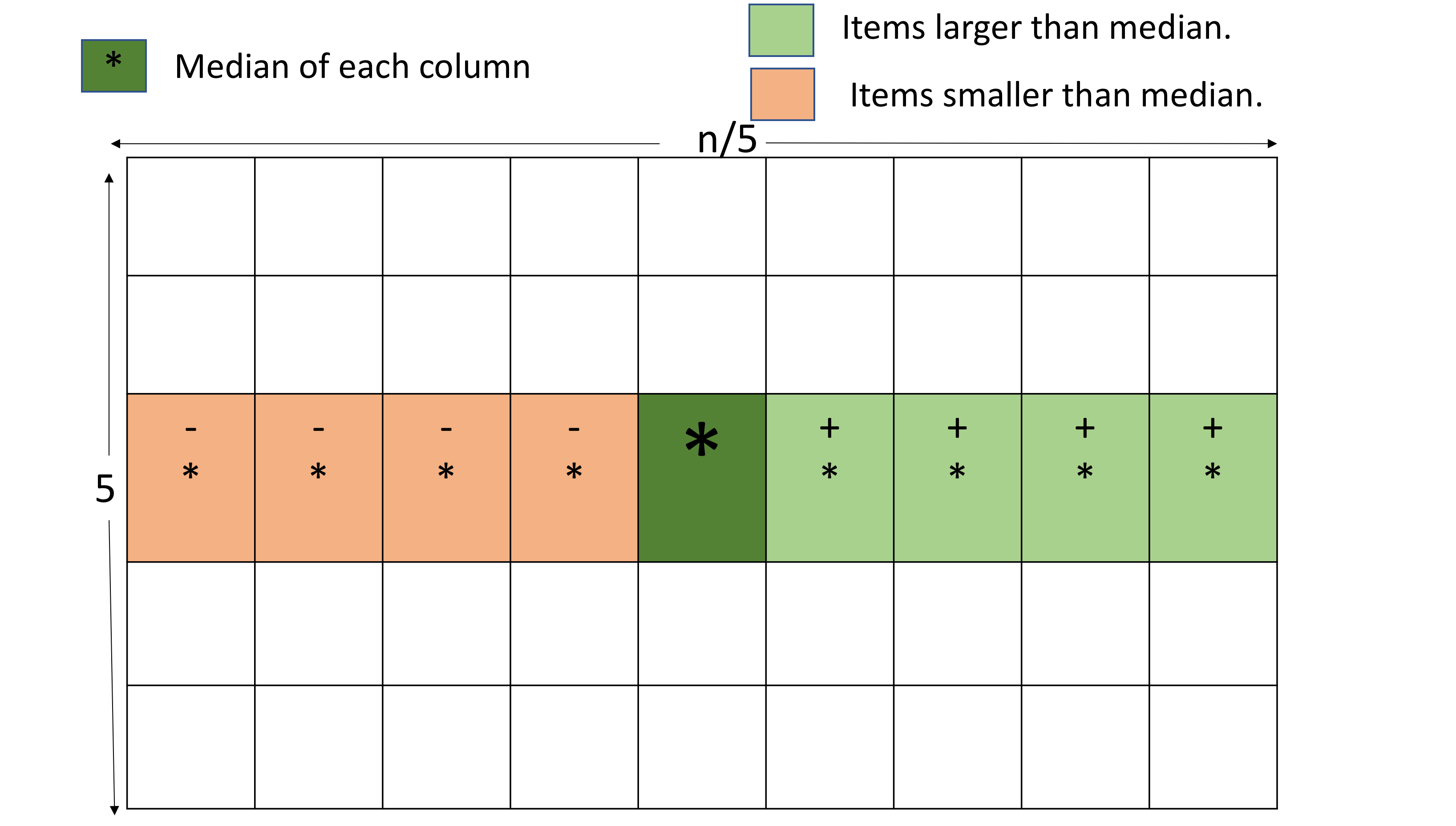
- Go through each element whose relationship to the big median is unknown and place it in the correct set.

For example:
Say, set1 = 31 elements (smaller)
set 2 = 68 elements (larger)
set1——median——-set2
31———–(32)———–68
50th biggest —> 50 – 32 = 18 –> Find the 18th biggest from set2, gives 50th biggest in the original. (note that this is recursive)
Analysis
Step 1: Partition Columns
6 comparisons each column, multiply by (n/5) columns
T(n) = 6(n/5)
Step 2: partition the middle row on the median and move the length 5 columns around appropriately.
- Finding median –> recursive call –> T(n/5)
- Move things around –> partitioning –> length of the array.
Every time we swap, we swap 5 elements, length = (n/5), swap = 5 for each –> (C1) some constant
so, T(n) = 6(n/5) + T(n/5) + C1(n/5)
Step 3: put unknowns to appropriate sets.
Worst case – (n/2) i.e half of the elements may be unknowns.
so, T(n) = 6(n/5) + T(n/5) + C1(n/5) + (n/2)
Step 4: Run the problem in set1 or set2 based on kth number(position).
Example: 31—-median(32)——-68
If we want 6th largest, run in set1.
Worst case = T(3n/4)
meaning, all unknown may fall into one set, making it 3/4th of the whole space, and we have to run our algorithm on that whole space.
When, set1: set2 = 25 : 75 , and the kth biggest element falls in set2, and hence worst case is 3/4th of the whole set.
Therefore, T(n) = 6(n/5) + T(n/5) + C1(n/5) + (n/2) + T(3n/4)
Hence, T(n) <= T((constant fraction) n)
Reference: Algorithms – Searching & Data Structures – Lecture 4